n <- seq(1,1E5,1000)
alpha <- 0.05
p1 <- 100E-6
p2 <- 500E-6
power <- power.prop.test(n = n, p1 = p1, p2 = p2, sig.level = alpha)
plot(power$n,power$power)
abline(h=0.8)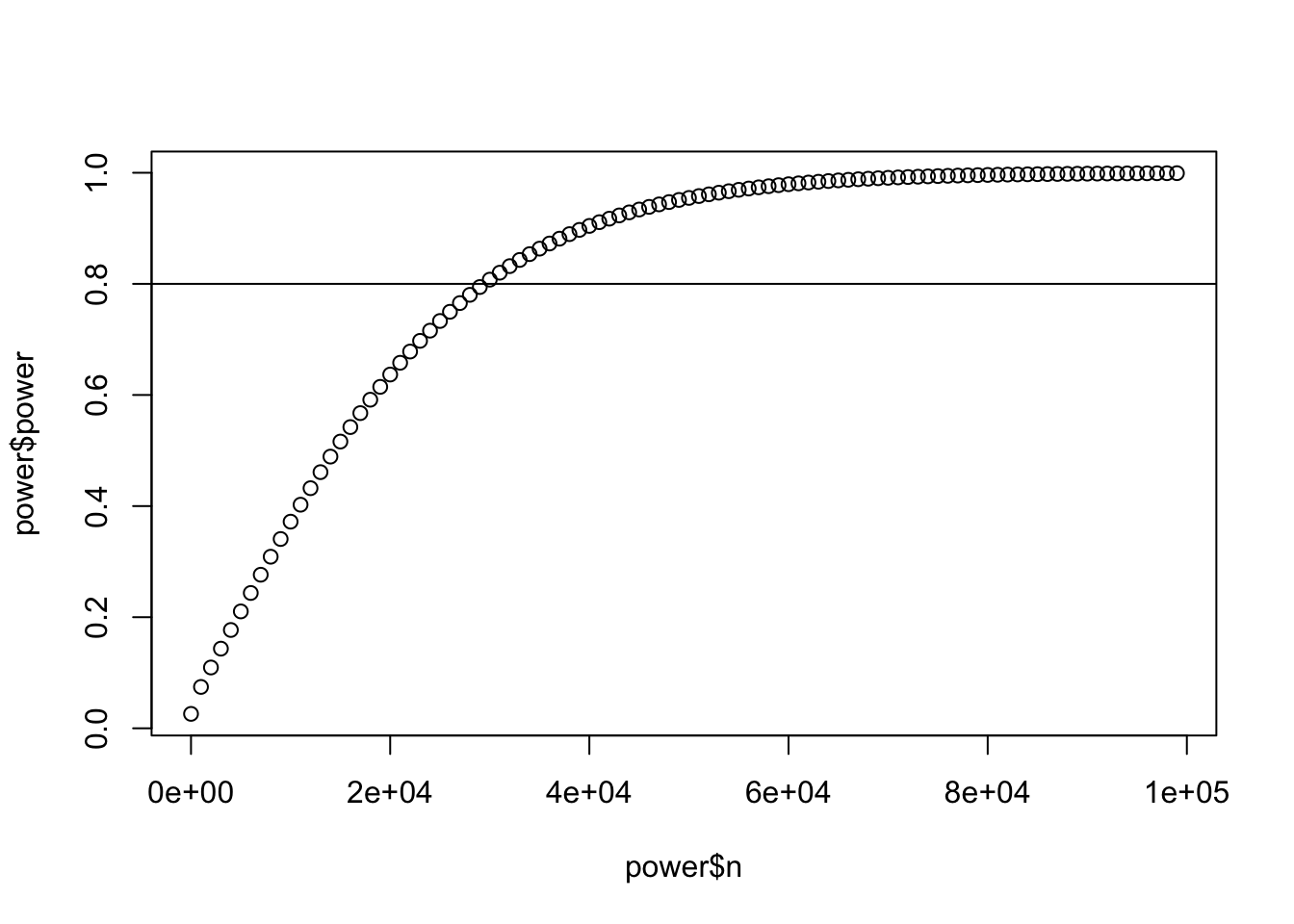
Nobukuni Hyakutake
2023-11-30

ここでは、0.8の検出力に線を引く。
It is proposed here as a convention that, when the investigator has no other basis for setting the desired power value, the value .80 be used.
出典: Statistical Power Analysis for the Behavioral Sciences Second Edition
n <- seq(1,1E5,1000)
alpha <- 0.05
p1 <- 100E-6
p2 <- 500E-6
power <- power.prop.test(n = n, p1 = p1, p2 = p2, sig.level = alpha)
plot(power$n,power$power)
abline(h=0.8)
n=29423のとき
n <- seq(1,1e3)
alpha <- 0.05
delta <- 0.01
sd <- 0.05
power <- power.t.test(n = n, delta = delta, sd=sd, sig.level = alpha)
plot(power$n,power$power)
abline(h=0.8)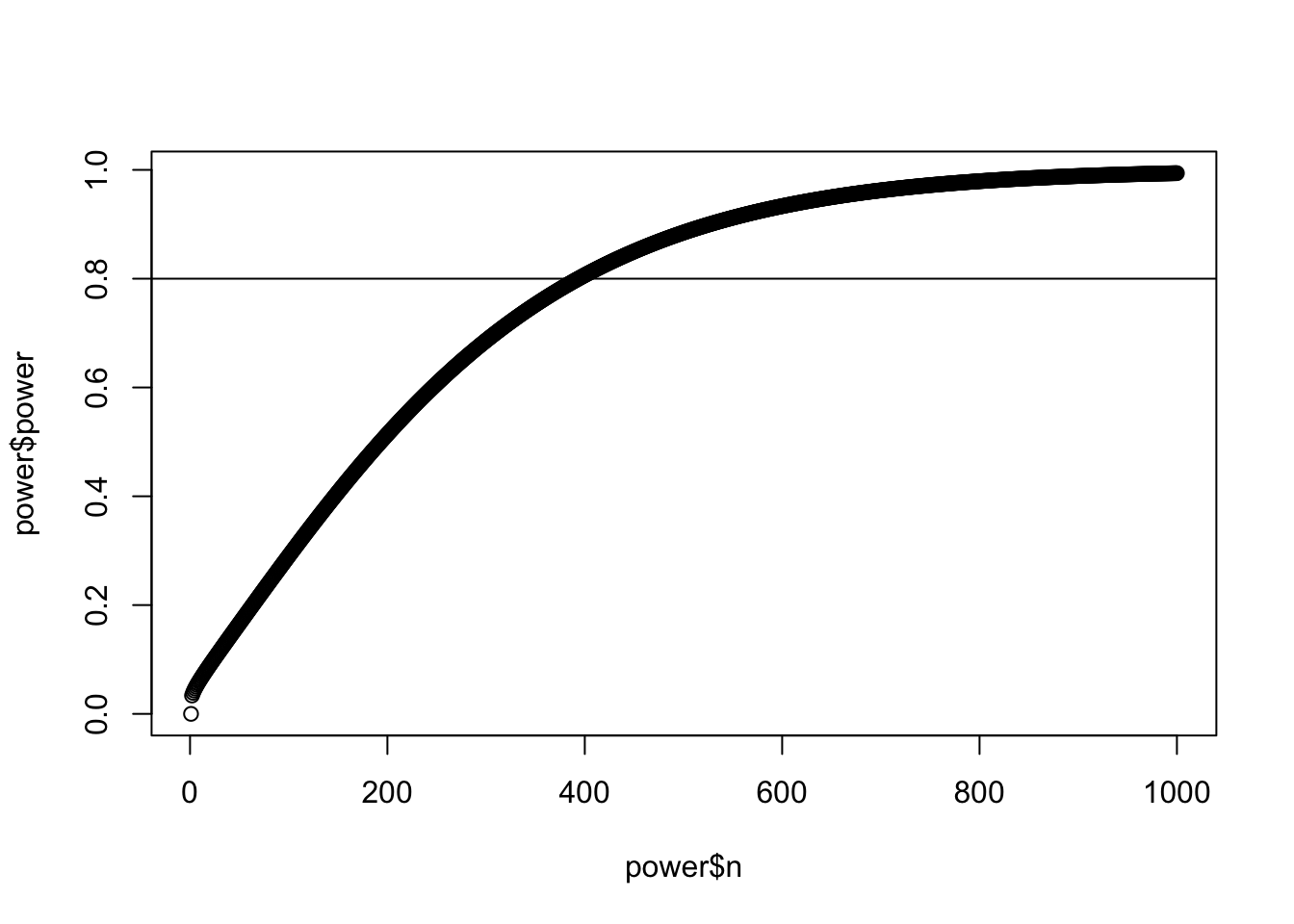
n=392のときの検出力
n <- seq(1,1e3)
alpha <- 0.05
delta <- 0.01
sd <- 0.05
power <- power.t.test(n = n, delta = delta, sd=sd, sig.level = alpha,type="paired")
plot(power$n,power$power)
abline(h=0.8)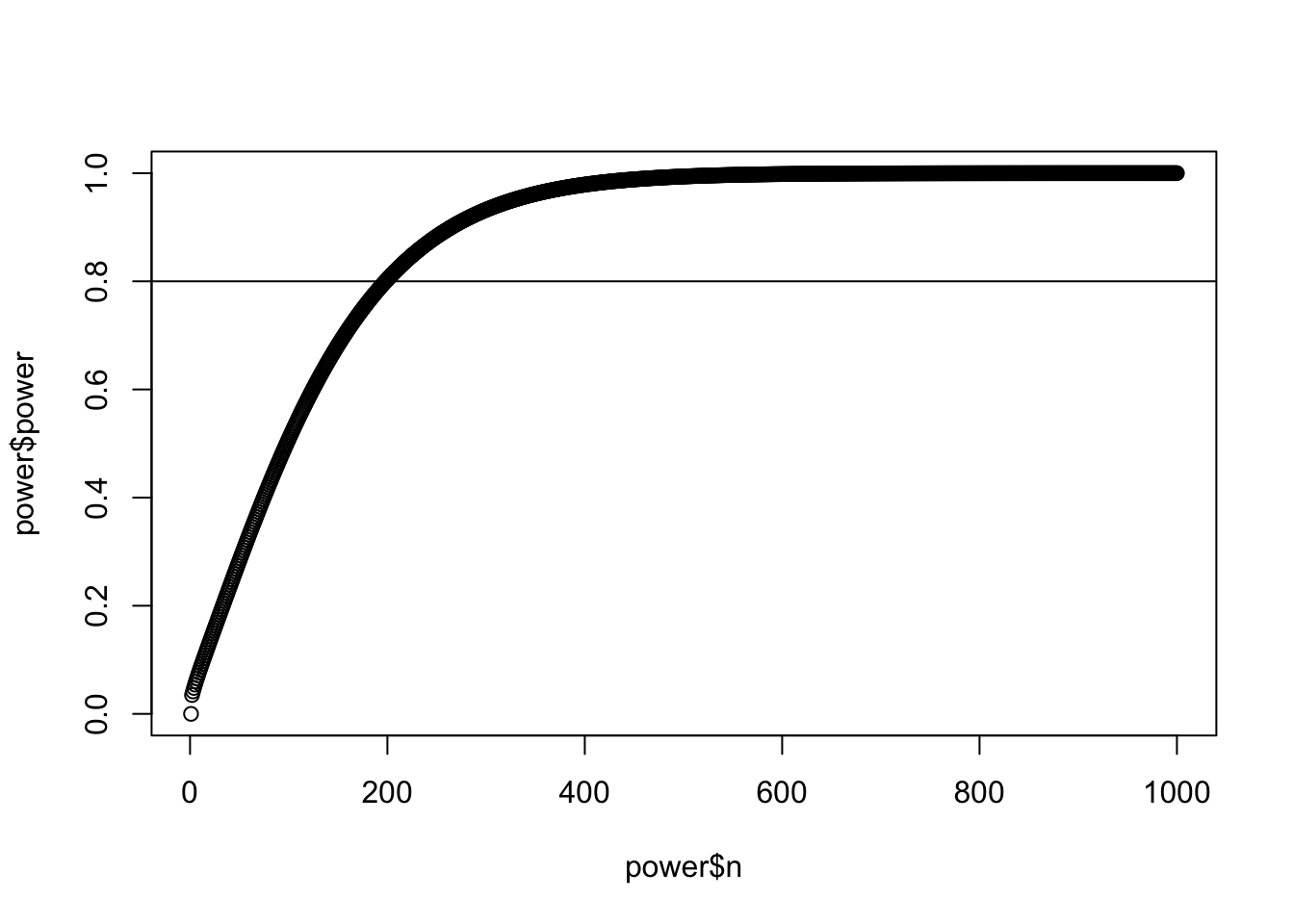
n=196のときの検出力
\[ n=\frac{\{Z(\alpha/2)\sqrt{2\overline{p}(1-\overline{p})}+Z(\beta)\sqrt{p_0(1-p_0)+p_1(1-p_1)}\}^2}{d^2} \]
\[ \overline{p}=(p_0+p_1)/2 \]
下記で計算する
\[ n=\frac{2\sigma^2\{Z(\alpha/2)+Z(\beta)\}^2}{d^2} \]
下記で計算する
\[ n=\frac{\sigma^2\{Z(\alpha/2)+Z(\beta)\}^2}{d^2} \]
---
title: "サンプルサイズ"
author: "Nobukuni Hyakutake"
date: "2023-11-30"
date-format: "iso"
categories: [R]
image: "lake.jpeg"
---

## power.prop.testの使い方
### 第一群の母比率𝑝1=100E-6、第二群の母比率𝑝2=500E-6、第一の過誤𝛼=0.05のときの母比率の差の検定の検出力
ここでは、0.8の検出力に線を引く。
> It is proposed here as a convention that, when the investigator has no other basis for setting the desired power value, the value .80 be used.
出典: [Statistical Power Analysis for the Behavioral Sciences Second Edition](https://www.utstat.toronto.edu/~brunner/oldclass/378f16/readings/CohenPower.pdf)
```{r}
n <- seq(1,1E5,1000)
alpha <- 0.05
p1 <- 100E-6
p2 <- 500E-6
power <- power.prop.test(n = n, p1 = p1, p2 = p2, sig.level = alpha)
plot(power$n,power$power)
abline(h=0.8)
```
n=29423のとき
```{r}
n <- 29423
alpha <- 0.05
p1 <- 100E-6
p2 <- 500E-6
power <- power.prop.test(n = n, p1 = p1, p2 = p2, sig.level = alpha)
power$power
```
### 第一群の母比率𝑝1=100E-6、第二群の母比率𝑝2=10000E-6、第一の過誤𝛼=0.05のときの母比率の差の検定の検出力
```{r}
n <- seq(1,1E4,100)
alpha <- 0.05
p1 <- 100E-6
p2 <- 10000E-6
power <- power.prop.test(n = n, p1 = p1, p2 = p2, sig.level = alpha)
plot(power$n,power$power)
abline(h=0.8)
```
### 観測数𝑛=10、母平均の差𝛿=0.1、標準偏差𝜎=0.05、第一の過誤𝛼=0.05のときの対応のないt検定の検出力
```{r}
n <- seq(1,100)
alpha <- 0.05
delta <- 0.1
sd <- 0.05
power <- power.t.test(n = n, delta = delta, sd=sd, sig.level = alpha)
plot(power$n,power$power)
abline(h=0.8)
```
### 観測数𝑛=10、母平均の差𝛿=0.01、標準偏差𝜎=0.05、第一の過誤𝛼=0.05のときの対応のないt検定の検出力
```{r}
n <- seq(1,1e3)
alpha <- 0.05
delta <- 0.01
sd <- 0.05
power <- power.t.test(n = n, delta = delta, sd=sd, sig.level = alpha)
plot(power$n,power$power)
abline(h=0.8)
```
n=392のときの検出力
```{r}
n <- 392
alpha <- 0.05
delta <- 0.01
sd <- 0.05
power <- power.t.test(n = n, delta = delta, sd=sd, sig.level = alpha)
power$power
```
### 観測数𝑛=10、母平均の差𝛿=0.1、標準偏差𝜎=0.05、第一の過誤𝛼=0.05のときの対応のあるt検定の検出力
```{r}
n <- seq(1,100)
alpha <- 0.05
delta <- 0.1
sd <- 0.05
power <- power.t.test(n = n, delta = delta, sd=sd, sig.level = alpha,type="paired")
plot(power$n,power$power)
abline(h=0.8)
```
### 観測数𝑛=10、母平均の差𝛿=0.01、標準偏差𝜎=0.05、第一の過誤𝛼=0.05のときの対応のあるt検定の検出力
```{r}
n <- seq(1,1e3)
alpha <- 0.05
delta <- 0.01
sd <- 0.05
power <- power.t.test(n = n, delta = delta, sd=sd, sig.level = alpha,type="paired")
plot(power$n,power$power)
abline(h=0.8)
```
n=196のときの検出力
```{r}
n <- 196
alpha <- 0.05
delta <- 0.01
sd <- 0.05
power <- power.t.test(n = n, delta = delta, sd=sd, sig.level = alpha,type="paired")
power$power
```
## サンプルサイズの計算
### 割合の差の検定(カイ2乗検定)
$$
n=\frac{\{Z(\alpha/2)\sqrt{2\overline{p}(1-\overline{p})}+Z(\beta)\sqrt{p_0(1-p_0)+p_1(1-p_1)}\}^2}{d^2}
$$
$$
\overline{p}=(p_0+p_1)/2
$$
#### 第一群の母比率𝑝0=100E-6、第二群の母比率𝑝1=500E-6、第一の過誤𝛼=0.05、検出力0.8としたときのサンプルサイズ
```{r}
alpha <- 0.05
p0 <- 100E-6
p1 <- 500E-6
power<-0.8
beta<-1-power
phat<-(p0+p1)/2
((-qnorm(alpha/2)*sqrt(2*phat*(1-phat))+(-qnorm(beta)*sqrt(p0*(1-p0)+p1*(1-p1))))^2)/((p1-p0)^2)
```
### 対応のないt検定のときのサンプルサイズ
下記で計算する
$$
n=\frac{2\sigma^2\{Z(\alpha/2)+Z(\beta)\}^2}{d^2}
$$
#### 標準偏差0.05, 検出すべき差を0.01,検出力0.8、$\alpha$を両側5%、検出力$1-\beta$を80%とした場合
```{r}
power<-0.8
alpha <- 0.05
delta <- 0.01
sd <- 0.05
(2*(sd^2)*(-qnorm(alpha/2)+(-qnorm(1-power)))^2)/(delta^2)
```
### 対応のあるt検定のときのサンプルサイズ
下記で計算する
$$
n=\frac{\sigma^2\{Z(\alpha/2)+Z(\beta)\}^2}{d^2}
$$
#### 標準偏差0.05, 検出すべき差を0.01,検出力0.8、$\alpha$を両側5%、検出力$1-\beta$を80%とした場合
```{r}
power<-0.8
alpha <- 0.05
delta <- 0.01
sd <- 0.05
((sd^2)*(-qnorm(alpha/2)+(-qnorm(1-0.8)))^2)/(delta^2)
```
## 参考文献
- [R言語 検出力・サンプルサイズ t検定や母比率の検定の検出力の計算](https://multivariate-statistics.com/2021/10/16/r-programming-power-sample-size/)
- [【pythonで統計学】統計検定のサンプルサイズを計算する](https://python-man.club/sample_size/)
- [サンプルサイズの設計](https://iss.ndl.go.jp/books/R100000002-I000011064467-00)
- [power.t.test() : 1群または2群のt検定のパワー計算をする関数](https://clover.fcg.world/2016/06/15/5302/)
## R version
```{r}
R.version.string
```