二乗平均平方誤差

目次

• 1 二乗平均平方誤差
  • 1.1 定義
  • 1.2 Graph (plotly)
  • 1.3 Graph (matplotlib)
  • 1.4 RMSE
• 2 平均二乗パーセント誤差の平方根（RMSPE：Root Mean Squared Percentage Error)
• 3 参考文献
• 4 Python version

1 二乗平均平方誤差

1.1 定義

\[ RMSE=\sqrt{\frac {\displaystyle\sum^{N}_{i=1}(予測値_i-実測値_i)^2} {N}} \]

1.2 Graph (plotly)

import numpy as np
import plotly.graph_objects as go
y_actual=np.array([33,35,36,39,50,44,41,51,56,50,47,52,49,55,55,51,61,58,58,57,66])
y_predicted=np.array([40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60])
scatter_trace=go.Scatter(x=y_actual,y=y_predicted,mode="markers",name="scatter")
line_trace=go.Scatter(x=np.array([40,60]),y=np.array([40,60]),name="linear")
fig=go.Figure([scatter_trace,line_trace])
fig

1.3 Graph (matplotlib)

import matplotlib.pyplot as plt
fig,ax=plt.subplots()
ax.plot(y_actual,y_predicted,'.')
ax.plot([40,60],[40,60],'-',color="green")
plt.show()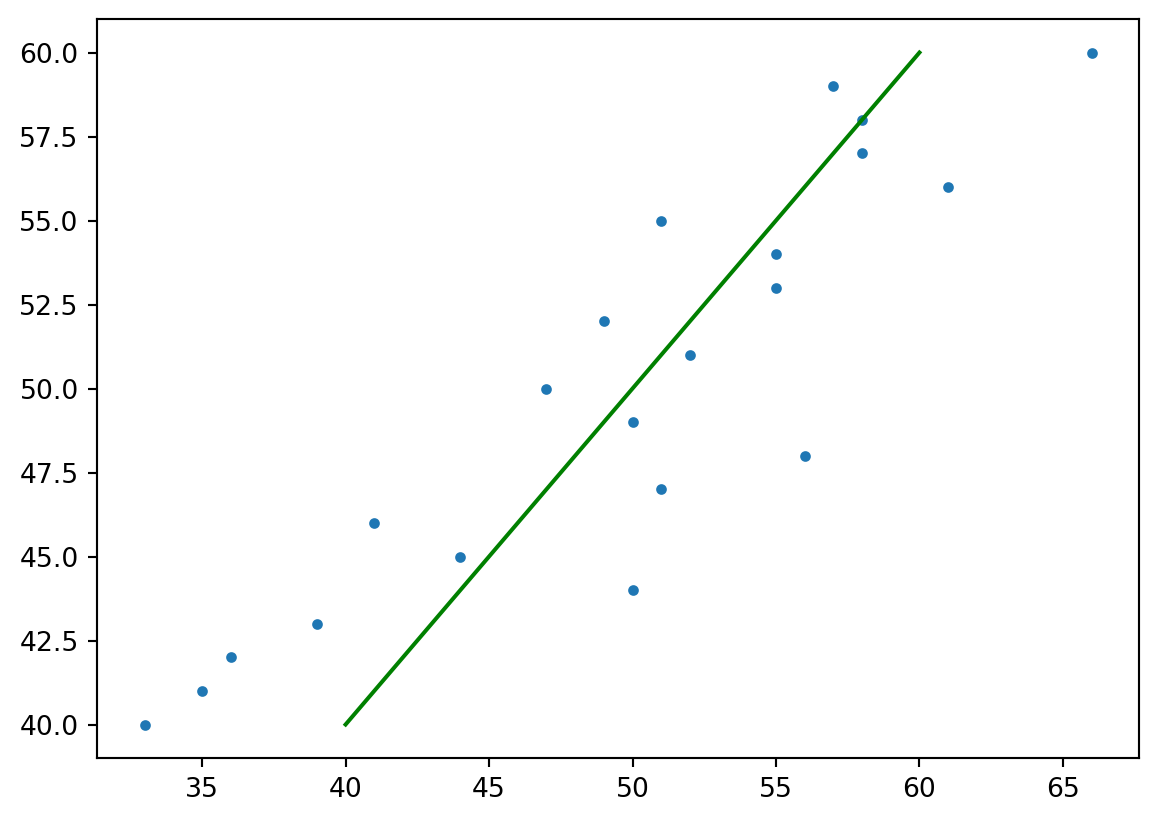

1.4 RMSE

from sklearn.metrics import mean_squared_error
from math import sqrt
rms=sqrt(mean_squared_error(y_actual,y_predicted))
print("RSME: "+str(round(rms,2)))

RSME: 4.29

2 平均二乗パーセント誤差の平方根（RMSPE：Root Mean Squared Percentage Error)

工事中です

3 参考文献

• 仕事ではじめる機械学習 第2版
• 評価指標入門 ~ データサイエンスとビジネスをつなぐ架け橋
• ［評価関数］平均二乗パーセント誤差の平方根（RMSPE：Root Mean Squared Percentage Error）とは？

4 Python version

import platform
"Python version "+platform.python_version()

'Python version 3.10.7'