library(tidyverse)
library(ggrepel)
g_width <- 100
g_height <- 100 * 2 / (1 + sqrt(5))
d01 <- read_csv("
point,value
1,0
2,1
3,2
4,3
5,-1
6,-2
7,-3
", show_col_types = FALSE)
d01$label <- as.character(d01$value)
d02 <- c(1 / 2, -3 / 2, sqrt(2), pi, -sqrt(3))
d03 <- tibble(
point = seq(8, 12),
value = d02,
label = c("frac(1,2)", "-frac(3,2)", "sqrt(2)", "pi", "-sqrt(3)")
) #?plotmath で文法は調べられる
d04 <- bind_rows(d01, d03)
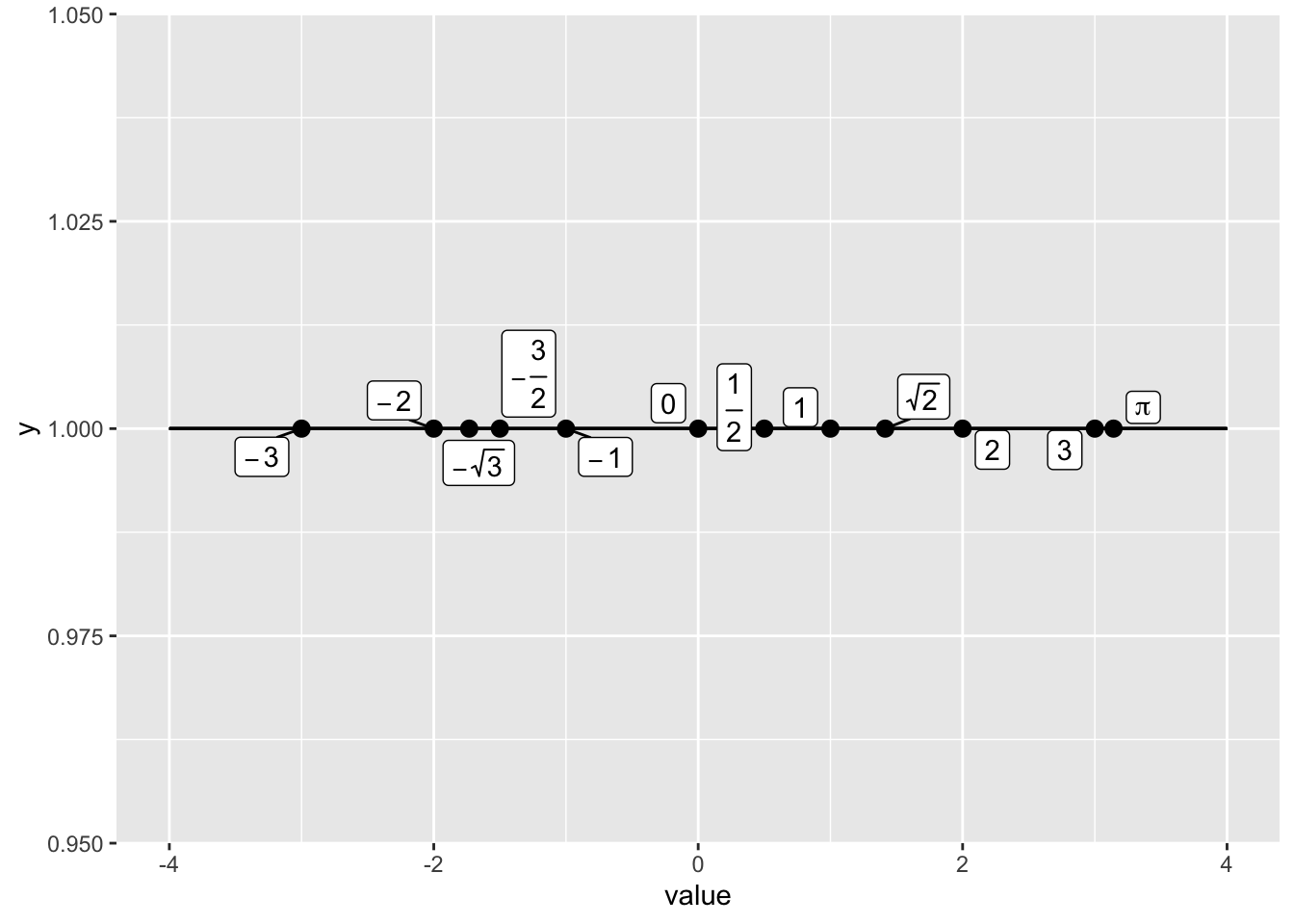
ggplot(d04, aes(value, 1, label = label)) +
geom_pointrange(aes(xmin = -4, xmax = 4)) +
geom_point() +
geom_label_repel(parse = TRUE)